Kosmoloogia - Dünaamika: Kuidas kaaluda taevakehi

4. osa: Galaktikad

[ Peatüki indeks | Õpiku tekst | Illustratsioonid | Viited | Kordamisküsimused ]

3. peatükk: Dünaamika

Kuidas kaaluda taevakehi
ERIK TAGO
Tänu üleüldisele külgetõmbele, mida kirjeldab Newtoni avastatud gravitatsiooniseadus, püsivad taevakehad koos. Tänu gravitatsioonile on nad Universumi arengu käigus üldse tekkinud. Sama seadus annab ka võimaluse mõõta taevekehade massi. Erinevate tähesüsteemide puhul tuleb aga kasutada erinevad viise, kuidas nende massi kindlaks teha. Enamus tahesüsteemide massi mõõtmisi põhineb nende dünaamikal, kusjuures eeldatakse, et need süsteemid on statsionaarsed (või kvaasistatsionaarsed, s.t. ajas väga aeglaselt muutuvad).
Maa ja Kuu mass
Taevakehade massi mõõtmise aluseks on Maa mass. Maa massi saame määrata Newtoni gravitatsiooniseadusest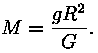 kus jõu F asendame valemist saame ehk avaldades Maa massi Gravitatsioonikonstant G on määratud füüsikalistest eksperimentidest (näiteks torsioonkaaludega), samuti ka raskuskiirendus g Maa pinnal (näiteks pendli võnkumisest). Asetades valemisse G, g ja Maa raadiuse R saame Maa massiks M_M = 6 * 10²⁷ grammi. Kuu mass leitakse tema liikumise täpsetest mõõtmistest ümber süsteemi Maa-Kuu masskeskme; Kuu mass M_K = M_M / 81,3 = 7,35 * 10²⁵ grammi.
Päikese ja planeetide massid
Newtoni poolt täpsustatud Kepleri kolmas seadus annab võimaluse kindlaks teha planeetide ja Päikese masse. Rakendades seadust nii süsteemile Maa-Kuu kui Päike-Maa saame seose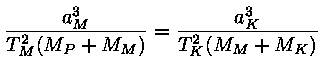 Lihtsustades võrrandid arvestusega, et Maa mass on tühine võrreldes Päikese massiga, saame Paremal pool on kõik vaatlustest saadavad suurused ning Kuu ja Maa mass, mille leidsime ülalpool. Tulemuseks saame M_P = 2 * 10³³ grammi ehk Päike on Maast 330 000 korda raskem.
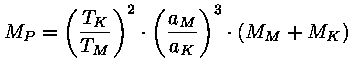
Tähe mass
Tähtede masse saab täpselt määrata kaksiktähtede korral. Rakendades jällegi Kepleri kolmandat seadust saame seose kaksiktähe summaarse massi jaoks (Päikese massi ühikutes):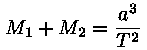 Siin on T ühe tähe tiirlemisperiood ümber teise tähe ja a tema orbiidi pikk pooltelg. Et leida kummagi tähe massi eraldi peame vaatlustest saama ka kummagi tähe kauguse ühisest masskeskmest; nende kauguste suhe annab masside pöördsuhte: Nende kahe seose põhjal saame määrata mõlema tähe massi. Et asi on tegelikult keerulisem, selles võib veenduda lisatekstist "Kaksiktähe kogumassi leidmine" ühe Suure Vankri kaksiktähe massi määramise näitest.
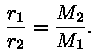
Tähtede masside määramine kaksiktähtede vaatlustest on küll kõige täpsem, kuid kahjuks saab sel viisil määrata vaid tühise osa tähtede masse. Lisaks sellele kasutatakse kaudseid tähtede massi hindamise meetodeid. Tänu statistilisele seosele tähtede massi ja heleduse vahel saab masside hinnanguks kasutada näiteks tähtede absoluutseid heledusi.
Masse saab määrata ka tähelt saabuva kiirguse gravitatsioonilise punanihke suurusest, mis on võrdeline tähe massiga ja pöördvõrdeline tähe raadiusega. See muidu väike efekt avaldub hästi valgete kääbuste korral (väikse raadiuse tõttu) ja annab võimaluse sõltumatult nende tähtede masse hinnata.
Galaktika mass
Spiraalgalaktikate massi (ning veel enamgi -- ka massijaotust) saab määrata galaktika pöörlemiskõverast (vt. lisatekst Pöörlemiskõver ja massi jaotus). Vaatleme siinkohal näitena, kuidas Päikese tiirlemisest ümber Linnutee keskme saab leida Linnutee massi. Eelduseks on siin, nagu eespool mainisime, Linnutee galaktika statsionaarsus. Lihtsustuseks loeme, et Päikese orbiit on ringjoon.
Mehaanikast ja gravitatsiooniseadusest saame (Päikesele mõjuv gravitatsioonijõud on võrdne talle mõjuva tsenrifugaaljõuga):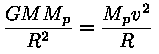
kus M_p, R ning v on Päikese mass, kaugus Linnutee keskmest ja orbitaalkiirus, M on Linnutee mass kauguseni R tsentrist (ainult see osa massist annab panuse Päikese liikumisse), G -- gravitatsioonikonstant. Avaldades massi ning asetades viimasesse avaldisse vaadeldud suurused v = 220 km/s ning R = 8,5 kpc saame Linnutee massiks Kogumass on veidi suurem välisosa arvel.
Elliptilised galaktikad ei pöörle (või kui, siis tühiselt) ning nende puhul sama meetodit ei saa kasutada. Siiski saab kasutada temasse kuuluvate tähtede liikumist massi dünaamiliseks hinnanguks. Sel puhul kasutatakse viriaali teoreemi, mida järgnevalt vaatamegi.
Galaktikaparve mass
Peamine meetod galaktikasüsteemide massi määramiseks on mehaanikast tuntud viriaali teoreem, mis seob süsteemi kuuluvate kehade summaarse kineetlise energia süsteemis toimivate jõududega. Statsionaarse isegraviteeruva süsteemi puhul (nagu seda eeldatakse olema kerasparvi, galaktikaid ja galaktikaparvi) taandub viriaali teoreem lihtsaks seoseks kineetilise ja gravitatsiooni potentsiaalse energia T ja W vahel: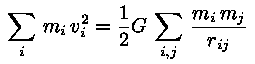 Avaldades kineetilise ja potentsiaalse energia saame : Näite lihtsustamiseks loeme galaktikate massid võrdseks. Siit saame seose kiiruste dispersiooni ning massi ja viriaalraadiuse vahel:
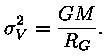
Näeme, et seos on analoogne pöörlemiskõvera rakendamisega, kus pöörlemiskiiruse osa on kiiruste dispersioonil ja pöörlemisraadiuse asemel on nn. viriaalraadius ehk harmooniline raadius. Vaatlustes saadakse kiiruste dispersioon ja süsteemi viriaalraadius ning leitakse süsteemi mass. Viriaalteoreemi rakendades on leitud, et galaktikaparved võivad olla 10 kuni 100 korda raskemad kui nendesse kuuluvate galaktikate summaarne mass (heleda aine mass). See on üks peamisi tõendeid varjatud ehk tumeda ehk nähtamatu aine olemasolust.
Dünaamikast sõltumatud massi mõõtmised
Meenutame, et dünaamilised massihinnangud põhinevad eeldustel, mis ei tarvitse siiski igal juhtumil kehtida. Peamine eeldus on süsteemi statsionaarsus. Kui aga see eeldus tegelikult ei kehti, saame süsteemi dünaamikast massi vale hinnangu. Kas on teisi sõltumatuid massi määramise viise, mis kinnitaksid varjatud aine vajadust? Õnneks tõesti on. Üheks meetodiks on galaktikaparve masse määrata kuuma röntgengaasi vaatlustest. Galaktikaparved sisaldavad 10 kuni 100 miljoni kraadist gaasi. Kui parved ei oleks piisavalt massiivsed, oleks neis sisalduv nii kuum gaas ammu haihtunud. Hüdrostaatilise tasakaalu võrrandist ja gaasioleku võrranditest saame avaldada massi vaadeldavate suuruste -- tepmeratuuri ning tiheduse ja temperatuuri gradientide -- kaudu. Tulemus näitab, et röntgengaasi põhjal saadud parvede massid on lähedased dünaamilistele määrangutele.
Teine sõltumatu meetod on gravitatsiooniläätse efekt. Galatikaparved on tugevad gravitatsooniläätsed ning kui nende taha samale vaatelkiirele satub kaugem galaktika või kvasar, siis saame nendelt tuleva valguskiire kõrvalekaldest mõõta parve massi. Seejuures efekti annab kogu parve mass ning see ei sõltu parve dünaamilisest olekust. Einsteini poolt leitud valemis on valguskiire kõrvalekaldenurk 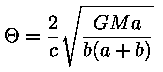seotud massi M ning parve (läätse) ja valgusallika kaugustega b ja a järgmiselt:

Mitmekümne galaktikaparve vaatlustest on saadud, et parved peavad sisaldama varjatud ainet. Seejuures on gravitatsiooniläätsede põhjal saadud massid keskmiselt 30% suuremad kui dünaamilised massid.
Seega need kolm sõltumatut meetodit kinnitavad vajadust tumeda aine järele.