Kosmoloogia - 4. osa: Galaktikad

[ Peatüki indeks | Õpiku tekst | Illustratsioonid | Viited | Kordamisküsimused ]

3. peatükk: Dünaamika

Pöörlemiskõver ja massi jaotus

JAAK JAANISTE
See, et me räägime galaktikate pöörlemisest, pole päris täpne. Pöörelda saab ikkagi ainult kõva keha; galaktikas võime rääkida vaid tähtede tiirlemisest ühise masskeskme -- galaktika tsentri ümber. See tiirlemine erineb oluliselt planeetide liikumisest: kuna galaktikat (erinevalt Päikesest) ei saa kuidagi lugeda punktmasssiks, ei kehti tähtede liikumisel ka Kepleri seadused.

Pöörlemiskõverast järeldub kaks asja: esiteks ei pöörle ketas nagu kõva keha (tegu on mitte tahke plaadi, vaid ühes tasapinnas liikuvate tähtedega, mis asuvad üksteisest küllaltki kaugel ja omavahel kuidagi seotud ei ole). Teiseks erineb nende tähtede liikumine galaktikas oluliselt planeetide liikumisest Päikese ümber: kui planeetide kiirus kahaneb võrdeliselt kaugusega tsentrist, siis tähtede liikumiskiirus galaktikas kas kasvab või ei muutu üldse.

Põhjuseks on erinevus massi jaotuses. Planeetide liikumist mõjutab peaasjalikult Päikese gravitatsiooniväli (planeetide massid on Päikese omaga võrreldes tühised), seevastu galaktika gravitatsioonivälja, mis juhib tema tähtede liikumist, tekitavad needsamad tähed ise. Selliste "isegraviteeruvate" süsteemide liikumist ja stabiilsust uurib astronoomia eriharu -- stellaardünaamika.

Mida siis näitab meie joonisel olev pöörlemiskõver? Ennekõike viitab see ainejaotusele galaktikas -- tiheduse sõltuvusele pöörlemistsentri kaugusest. Iga tähe liikumise määrab gravitatsioonijõu ja tsentrifugaaljõu vahekord; kui need on kogu aeg võrdsed, liigub täht ringjoonelisel orbiidil; kui mitte, siis piki ellipsit. Erijuhul, kui pöörlemist ei ole (tsentrifugaaljõud puudub), võngub täht gakaktika keskme suhtes edasi-tagasi. Selliseid orbiite nimetatakse radiaalseteks.

Oletame, et ainetihedus galaktikas sõltub tsentri kaugusest astmefunktsiooni järgi. Püüame rehkendada, milline pöörlemiskõvera kuju vastab erinevatele astmenäitajatele.

Kirjeldagu tiheduse radiaalset muutumist funktsioon

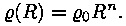roo(R) = roo_0 * R^n.
Võtame kaugusel R tsentrist ringorbiidil kiirusega v liikuva tähe. Sellele mõjub tsentrifugaaljõud
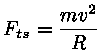F_ts = m * v^2 / R
ja gravitatsioonijõud
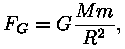F_G = G * (M * m / R^2),
mis peavad olema võrdsed. Massi M leiame, liites kokku kõigi nende tähtede massid, mis asuvad meie poolt vaadeldava tähega võrreldes tsentrile lähemal. Kui tähtede tihedus oleks kõikjal ühesugune, tuleks korrutada raadiusele vastava kera ruumala tähtede ruumtihedusega (tähtede arvuga ruumalaühikus); et tähtede tihedus aga raadiuse kasvades muutub, tuleb meil massi leidmiseks arvutada integraal. Selleks leiame kõigepealt tähtede kogumassi mingis õhukeses sfäärilises kihis raadiusega R ja paksusega dR. 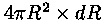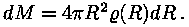Selle kihi ruumala on 4 * pii * R^2 * dR (sfääri pindala korda kihi paksus) ja kihti jäävate tähtede mass dM = 4 * pii * R^2 * roo(R) * dR. Ülaltoodud astmefunktsioonist lähtudes saame massi integraalist
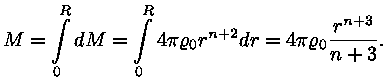M = integraal rajades 0-st R-ni (dM) = integraal rajades 0-st R-ni (4 * pii * roo_0 * r^(n+2) * dr) = 4 * pi * roo_0 * r^(n+3) / (n + 3).
Jõudude tasakaalu võrrandi saame nüüd kujul
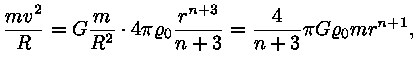m * v^2 / R = G * (m / R^2) * 4 * pii * roo_0 * (r^(n+3) / (n + 3)) = (4 / (n+3)) * pii * G * roo_0 * m * r^(n+1),
millest
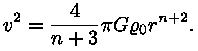
v^2 = (4 / (n + 3) * pii * G * roo_0 * r^(n+2).

Selle valemi abil saame teha ilusa tabeli, millega võime analüüsida massijaotust pöörlemiskõrvera järgi:

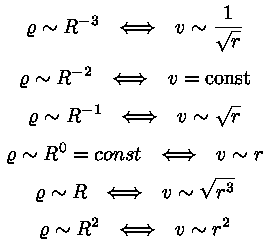roo ~ R^(-3) <==> v ~ 1 / ruutjuur(r); roo ~ R^(-2) <==> v = const; roo ~ R^(-1) <==> v ~ ruutjuur(r); roo ~ R^0 = const <==> v ~ r; roo ~ R <==> v ~ ruutjuur(r^3); roo ~ R^2 <==> v ~ r^2
jne.

Näeme, et kriitiliseks astmenäitajaks on n = -2. Sellest kiirem tiheduse langus (n < -2) annab langeva pöörlemiskõvera (kiirus väheneb kauguse suurenedes), aeglasem (n > -2) aga tõusva kõvera (kiirus suureneb väljapoole liikudes). Konstantsele tihedusele vastab raadiusega võrdeliselt kasvav pöörlemiskiirus; nurkkiirus 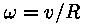oomega = v / R on seega konstantne -- galaktika pöörleb kõva kettana.

[foto1]
Foto 1. Spiraalgalaktika NGC 2998 foto. Tume rõhtjoon näitab spektrograafi pilu asendit.

[foto2]
Foto 2. Sama galaktika spekter. Keskmises mõhnale vastavas osas näeme kaootilistele liikumistele tüüpilisi laienenud jooni; äärtel on jooned tsentri suhtes sümmeetriliselt nihkunud - seal asub pöörlev õhuke ketas.

[joonis2]
Joonis 1. NGC 2998 pöörlemiskõver -- tähtede kiirused sõltuvalt tsentri kaugusest.

[joonis3]
Joonis 2. Varbspiraalse galaktika pöörlemiskõver: keskosas on tähtede kiirus võrdeline kaugusega tuumast.

[ Peatüki indeks | Õpiku tekst | Illustratsioonid | Viited | Kordamisküsimused ]

Õpiku tegijad / opik@obs.ee
© Tartu Tähetorni Astronoomiaring 1997-98

22. märts 1998

 [Avatud Eesti Fond]

Selle õpiku valmimist on toetanud Avatud Eesti Fond.