Kosmoloogia - 1. osa: Maa ja taevas

[ Peatüki indeks | Õpiku tekst | Illustratsioonid | Viited | Kordamisküsimused ]

4. peatükk: Planeedid tähistaevas

Taevakehade liikumine

JAAK JAANISTE

1563. aastal, jälgides Jupiteri ja Saturni kohtumist taevalaotuses, märkas noor astronoom Tyco Brahe, et astroloogilistes tabelites on planeetide liikumine kirjeldatud vigaselt. Soov tabeleid parandada viis Brahe aastatepikkuste taevavaatluste juurde. Kolmkümmend aastat kestnud, tolle aja kohta ülitäpsete planeedivaatluste tulemused pärandas ta oma õpilasele Johannes Keplerile.

1609. ja 1619. a. ilmunud teostes "Astronomia Nova" ning "Harmonica Mundi" formuleeris Kepler (1571 - 1630) planeetide liikumise kolm seadust:

  1. Planeedi liikumistee (orbiit) on ellips, mille fookuses on Päike.
  2. Planeedi raadiusvektor (lõik Päikesest planeedini) katab võrdsetes ajavahemikes võrdsed pindalad.
  3. Planeetide tiirlemisperioodide ruudud suhtuvad nagu nende orbiitide pikemate pooltelgede kuubid.

[Joonis] Joonis: ellips, fookus, poolteljed, raadiusvektor ja selle poolt kaetud pindala.

Kepler tuletas oma seadused isiklike ning oma õpetaja ja eelkäija Tycho Brahe poolt tehtud täpsete vaatluste põhjal. Seetõttu tuleb neid käsitleda kui empiirilisi, vaadeldavate parameetrite vahelisi seoseid. 1687. a. näitas I. Newton, et Kepleri seadused on range matemaatiline järeldus tema poolt formuleeritud ülemaailmsest gravitatsiooniseadusest: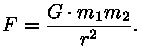

Mistahes kaks keha tõmbavad teineteist jõuga, mis on võrdeline nende kehade massidega ja pöördvõrdeline nende vahelise kauguse ruuduga. Valemina:
F = (G * m_1 * m_2) / r^2.

Et selles veenduda, tuleks meil lahendada nn. ühe keha probleem -- arvutada tsentraalsümmeetrilises jõuväljas liikuva keha trajektoor (leida liikumisvõrrand). Kuigi seda loetakse üheks lihtsamaks mehaanikaülesandeks, napib meil tema täpseks lahendamiseks matemaatika-alaseid oskusi. Aga midagi me siiski suudame.

Olgu meil välja allikas -- punktmass massiga M ning suvaline liikuv keha massiga m ja kiirusega vektor v. Sellele kehale mõjub gravitatsioonijõud vektor F, mis on suunatud tõmbetsentri M poole.

Üldjuhul, kui keha kiirusvektor pole suunatud piki liikuvat keha tõmbetsentriga ühendavat sirget, määravad kiirusvektor ja jõuvektor tasandi, millel toimub keha liikumine. Jagame jõuvektori kaheks komponendiks, millest üks on suunatud kiirusvektoriga paralleelselt, teine aga sellega risti. Need jõud sunnivad keha liikuma kiirendusega, kusjuures kiirusega paralleelne kiirenduse komponent muudab kiiruse suurust, temaga risti olev aga liikumissuunda. Just viimase tõttu hakkabki keha liikuma piki kõverjoont, milleks võib olla ringjoon (kui paralleelne komponent on kogu aeg null) või ellips. Aga mitte ainult ellips.

Jõuväljas liikuva keha energia koosneb kahest osast: kineetilisest ja potentsiaalsest energiast. Esimene neist on alati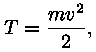

T = m * v^2 / 2,
teine sõltub jõuvälja iseloomust. Punktmassi gravitatsiooniväljas on potentsiaalne energia
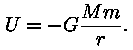
U = - G * (M * m) / r.

Miinusmärk tähendab, et kauguse r suurenemisel potentsiaalne energia väheneb, saades nulliks lõpmata kaugel valja allikast. Potentsiaalse energia märk on kokkuleppeline: energia jäävuse seadusest teame, et keha energia suurendamiseks tuleb teha tööd, nii ka proovikeha väljaviimisel gravitatsiooniväljast. Et kauguse suurenemise tulemusena saab energia nulliks (U --> 0, kui r --> lõpmatus), peab ta algul olema negatiivne.

Energia jäävuse seadus nõuab, et E = T + U = const. Et keha ei jõuaks tõmbetsentrist kaugemale, kui orbiit võimaldab, peab E < 0 ehk T < U. Siis on liikumisteeks ellips (või erijuhul ringjoon) ja kehtivad Kepleri seadused. Aga kui ei ole?

Ellips ja ringjoon on mõlemad teist järku kõverad. Selliseid kõveraid nimetatakse koonuslõigeteks (ringjoon tekib, kui lõikame koonilist pinda selle teljega risti oleva tasandiga, ellips aga siis, kui tasand on teljega nurga all). Aga koonust saab lõigata ka nii, et kinnist joont ei teki.

Kui E = 0, tekib joon, mille lõikab koonilisest pinnast tasand, mis on paralleelne moodustajaga. Seda joont nimetatakse parabooliks. Piki parabooli liiguvad gravitatsiooniväljas need kehad, mille potentsiaalne energia on täpselt võrdne kineetilise energiaga. Nii liigub enamik komeete.

Kui E > 0, tekib hüperbool -- kõver, mis kujutab tõmbetsentrist suure kiirusega mööda lendava keha suunamuutust (ka see on koonuslõige, mõelge välja, millise tasandiga!). Hüperboolseks võib ligikaudu lugeda näiteks kosmoseaparaatide Voyager trajektoore Jupiterist või Saturnist möödumisel.

[Joonis] Joonis: Kosmilise trajektoori tüüp sõltub gravitatsiooniväljas liikuva keha kineetilisest energiast T, see omakorda kiirusest v.

Niipalju siis kõige lihtsamast ülesandest. Kaasaegne taevamehaanika, planeerides planeetidevahelisi lende, saab hakkama ka kahe, kolme ja enama keha liikumise arvutamisega.

[ Peatüki indeks | Õpiku tekst | Illustratsioonid | Viited | Kordamisküsimused ]

Õpiku tegijad / opik@obs.ee
© Tartu Tähetorni Astronoomiaring 1997

28. veebruar 1998

 [Avatud Eesti Fond]

Selle õpiku valmimist on toetanud Avatud Eesti Fond.