Kosmoloogia - Füüsikalised parameetrid: Kaksiktähe kogumassi leidmine

3. osa: Tähed

[ Peatüki indeks | Õpiku tekst | Illustratsioonid | Viited | Kordamisküsimused ]

3. peatükk: Füüsikalised parameetrid

Kaksiktähe kogumassi leidmine
JAAK JAANISTE

Taevas on miljoneid tähti, mis koosnevad kahest või mitmest ühise masskeskme ümber tiirlevast tähest. Vähemalt üks selline paar -- Suure Vankri teine aisatäht Mizar/Alkor (rahvaastronoomia Härg ja Hunt) on eristatav ka palja silmaga. Kahjuks asuvad need teineteisest liig kaugel, et kaaslase liikumine peatähe suhtes märgatav oleks. Küll on aga Suure Vankri -- täpsemalt küll Karu -- lõunapiiril täht 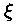, mis teleskoobis samuti kaksikuna paistab ning mille kaaslane on pärast avastamist 1826. a. juba poolteist tiiru ära teinud.
Kui tahame määrata 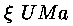massi, peame teadma tema komponentide orbiite (vähemalt nende pikemaid pooltelgi a) ning tiirlemisperioodi T. Siis saaksime leida Kepleri kolmanda seaduse konstandi A
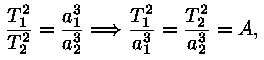(T_1)^2 / (T_2)^2 = (a_1)^3 / (a_2)^3 ==> (T_1)^2 / (a_1)^3 =
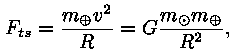(T_2)^2 / (a_2)^3 = A, mille väärtus on teada Päikesesüsteemist, näiteks Maa liikumisest. Maa püsib orbiidil tänu gravitatsioonijõule, mis tasakaalustab liikumisel tekkiva tsentrifugaaljõu: F_ts = m_oplus * v^2 / R =G * m_odot * m_oplus / R^2, kus Maa kaugus Päikesest R on ringorbiidi raadius, mis teadupoolest vastab ellipsi pikemale poolteljele. 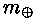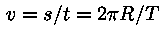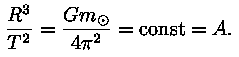Kui valemi mõlemad pooled Maa massiga läbi jagada ning kiirus v asendada valemist (T on Maa tiirlemisperiood), saame valemi R^3 / T^2 = G * m_opunkt / (4 * pii^2) = const = A.
Konstant on konstant ja kui panna R ja T asemele meie tähe parameetrid a ja T, tuleks teises pooles asendada vaid mass. Gravitatsioonikonstant G ja matemaatiline konstant 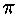on universaalsed (vähemalt nii me arvame), seega saamegi valemi tähe massi arvutamiseks:
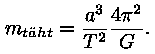
m_täht = (a^3 / T^2) * (4 * pii^2 / G).
Valem on käes, kahjuks ei tea me a väärtust. Meil on vaid tähe kaaslase näiva liikumise pilt taevasfääril. Ja seegi, nagu pildil näha, kaunis karvane. Pole ime -- orbiidiellipsi läbimõõt on vaid viis kaaresekundit (võrdle Tartu teleskoobi piirtäpsuse, 0,25"-ga). Ja ometi on pooltelg selle joonisega täpselt määratud (muidugi eeldusel, et tähe kaugus on teada).
Kõigepealt tuleb leida orbiidi kaldenurk vaatesihi suhtes. Ei maksa loota, et see on täisnurk (ainult siis vastab orbiidi tegelik kuju vaadeldavale ellipsile). Õnneks ütleb Kepleri I seadus, et teine täht asub orbiidi fookuses. Meie tähel see nii ei ole (näiva ellipsi fookus on märgitud ristiga), järelikult on orbiit kaldu. Aga mis suunas ja kui palju? Anname kaks erijuhtu:

Kui orbiit on ringikujuline, asub tsentraalne täht vaadeldava ellipsi tsentris.
Kui orbiidi pooltelg projekteerub vaatesuunale, on tsentraalne täht ka näiva ellipsi poolteljel.
Meie tähele ei kõlba kumbki. Et probleemi lahendada, tuleb appi võtta Kepleri II seadus ja aastamärgid. Proovige, kas saate hakkama.
Ja veel üks mõistatus: me ei tea, millised on kaksiktähe komponentide massid. Kui nad on lähedased, ei tiirlegi "kaaslane" peatähe ümber, vaid mõlemad liiguvad ümber ühise masskeskme. Et see asub tähtede vahel, on orbiidi tegelik pooltelg lühem vaadeldavast.
Milline oleks väljapääs? Teeme kaks joonist. Ülemine on nn. masskeskme süsteemis: mõlemad tähed (A ja B) liiguvad ümber masskeskme O. Teine on tähega A seotud süsteemis. Indeksid näitavad tähtede asendit eri ajamomentidel. Kõik orbiidid on ellipsid.
Millal on joonised a) ja b) identsed? Aga juhul, kui kogu tähti A ja B orbiidil hoidev mass on koondunud tähte A, st. kui 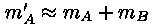ja 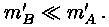Meil ei jäägi üle muud, kui oletada, et see nii on. Mass, mille me oma valemitest saame, on tegelikult kaksiktähe komponentide masside summa.
Kas on võimalik teada saada ka komponentide masse? On, kui leiame tähtede kiirused orbiidil. Aga kuidas?
Kas on huvitav ülesanne?

Joonis 1. Suure Karu kaksiktähed: (Mizar ja Alkor) ning .

Joonis 2. kaaslase näiv liikumine.

Joonis 3. Silutud orbiit: rist tähistab näiva ellipsi fookust.

Joonis 4. Kaksiktähe komponentide orbiidid: a) masskeskme suhtes; b) peatähe A suhtes.