Kosmoloogia - 5. osa: Universum

[ Peatüki indeks | Õpiku tekst | Illustratsioonid | Viited | Kordamisküsimused ]

4. peatükk: Kosmoloogilised mudelid

Suure hulga vaatlusandmete olemasolu ühelt poolt ja lõputu maailmaga seotud probleemid teiselt poolt kutsuvad teadlasi-uurijaid püstitama oletusi (hüpoteese), mis aitaksid vältida teooria paradokse, jäädes samal ajal kooskõlla kõigi kättesaadavate vaatlusandmetega. Selliseid kindlatel lähte-eeldustel põhinevaid kogu Universumi arengut kirjeldavaid teooriaid nimetatakse kosmoloogilisteks mudeliteks. Me ei pööra tähelepanu varasematele katsetele vältida üht või teist paradoksi (neeldumishüpotees, fluktuatsioonihüpotees), vaid asume kohe tänapäevase põhimudeli juurde.

Paisuv ruum on see võlusõna, mis ühel hoobil kõrvaldab kõik kolm paradoksi. Ruumi paisumine tähendab kõikide vahekauguste sõltuvust ajamomendist, täpsemalt nende ajalist kasvu. See kasv ei ole mingil määral seotud kehade liikumisega, ta peab olema kõigis suundades ühtlane ning soovitavalt ajas muutumatu (et rahuldada kosmoloogilist printsiipi). Põhjus, miks kõik kaasaegsed teooriad seda arvestavad, on vaatluslikku laadi: Hubble'i seadus (kaugusega võrdeline punanihe galaktikate spektrites) on otsene füüsikaline järeldus paisuvast ruumist. Tähendab ju paisumine seda, et iga mingit kaht eset eraldava ruumi meeter suureneb igas sekundis kindla murdosa võrra; seetõttu kaugenevad kõik esemed vaatlejast kiirustega, mis on võrdelised nende kaugusega. Punanihe aga on Doppleri efekti kohaselt just eemaldumiskiiruse näitaja.

Igapäevaelus me midagi sellist ei märka. Ja ei peagi märkama, sest tegu on kosmilise seadusega, mis avaldub alles väga suurte kauguste korral. Hubble'i seaduse võrdeteguri -- Hubble'i konstandi -- väärtus on praegustel andmetel 50...80 km / s Mpc ehk SI-süsteemi teisendatuna 2 * 10-18 m/s meetri kohta. Piltlikult väljendades vastab selline paisumine maakera läbimõõdu kasvule ühe mikromeetri(!) võrra aastas. Pealegi ei tähenda ruumi paisumine sugugi seal olevate kehade ruumala suurenemist, piisab vaid nende vahelise kauguse muutumisest.

Paradokside kõrvaldamiseks on sellisest paisumisest enam kui küllalt. Juba suhteliselt väike (lõpmatusega võrreldes!) piirkond raadiusega 5000 Mpc paisub ligikaudu valguse kiirusega; meie graafikul fotomeetrilise paradoksi kohta (vt. joonist) on see nii väike, et ei mahu isegi joonisele. Kuna neilt "minema jooksvatelt" tähtedelt pole oodata mingit erilist valgust, siis taevas on ja jääbki pimedaks. Kaob ka termodünaamiline paradoks: kuipalju me ilmaruumi ka ei soojendaks, adiabaatilise protsessi valemite järgi jahutab paisumine teda ikkagi rohkem, kui soojendana toimiv kohalik gravitatsiooniline kuhjumine teda kütta jõuab. Nii et soojusmasin töötab täie auruga. Ka gravitatsiooniline paradoks kaotab oma hambad, kuna tihedamate alade kokkulangemise kiirus jääb suurtes mastaapides alati alla ruumi paisumisele. Kokkulangemine kohalikus mastaabis ei oma aga Universumi arengu seisukohalt mingisugust tähtsust.

Võtame kokku: paisuv ruum on vaatluslik fakt, mis on suuteline kõrvaldama kõik "lõpmatu maailma" paradoksid. Jääb üle vaid viia see fakt kooskõlla füüsika seadustega. Seda teevadki kosmoloogilised mudelid, igaüks neist oma kombel. Vaatame kolme neist lähemalt.

1. Statsionaarne mudel. (F. Hoyle ja H. Bondi, 1948). Kas on üldse võimalik luua paisuva ruumiga mudelit, mis rahuldaks kosmoloogilist printsiipi? Tuleb välja, et on küll. Selleks tuleb teha oletus, et ainetihedus paisuvas ruumis jääb konstantseks. Kuna tihedus arvutatakse valemiga roo = m / V, V aga suureneb, peab koos mingi ruumiosa paisumisega suurenema ka sellesse ruumiossa jääv mass. Teiste sõnadega, et säiluks keskmine tihedus, peab paisuv ruum ainet juurde tekitama. Siin me ohverdame teadlikult tükikese harjumuspärast füüsikat (aine jäävuse seaduse), aga jällegi ainult kosmilises mastaabis. Katseliselt, st. laboris on seda efekti (massi juurdekasvu) niisama võimatu mõõta, kui kosmilist pikenemistki (m = roo * V = roo * R^3; (Delta m) / m = (Delta V) / V = ((Delta R) / R)^3 = 10^(-33) kilogrammi aastas kilogrammi kohta!)

Tuleb lisada, et tegu on väga kavala mudeliga, kus kosmoloogiline printsiip on rahuldatud täielikult ja lõplikult: ta on postulaadina kodeeritud teooria olemusse. Sellele vaatamata pole mudel astrofüüsikute seas populaaarne. Mitte, et ta halb oleks -- aga on paremaid mudeleid, mis on suutelised kirjeldama suuremat faktide hulka.

2. Graviteeruv mittestatsionaarne mudel (E. Milne 1934) võtab aluseks galaktikate laialilendamise fakti ning esitab selle matemaatilise kirjelduse tavalise ruumi ning Newtoni mehaanika kaudu. Milne'i mudelis ei paisu ruum, küll aga lendavad selles ruumis laiali galaktikad ja teised kosmilised objektid. Mudel ei tungi Universumi olemusse, vaid üksnes kirjeldab galaktikate vaadeldavat liikumist.

Newtoni valemid ei võimalda kirjeldada lõpmatu keskkonna käitumist. Aga me võime alati teha matemaatilise nipi: rehkendada kõigepealt lõplikku piirkonda, ja siis, kui lahend juba käes, üldistada seda suurematele kaugustele, kuni lõpmatuseni välja. Ühtlase tihedusega rõhuvaba ainega (tolmuga) täidetud kera kokkutõmbumise valemi võib igaüks kirja panna; et algebralised seosed on pööratavad, saame sellest teha ka paisuva tolmupilve valemi. Kui jagada kera paisumiskiirus kera raadiusega, saamegi Hubble'i konstandi -- kauguse juurdekasvu ajaühikus e. kiiruse ühikulise vahemaa jaoks (vt. lisateksti). Ainult et see "konstant" polegi konstantne, vaid muutub ajas valemi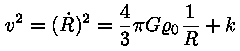

v^2 = (R')^2 = (4 / 3) * pi * G * roo_0 * (1 / R) + k
järgi. See paisumiskiirus väljendabki Universumi ajalist arengut. Statsionaarsele olekule, kus maailm ei paisu, vastab R = const ehk R' = 0. See on võimalik kahel juhul, sõltuvalt integreerimiskonstandi k väärtusest:

  1. k = 0, R --> lõpmatus

    Seda nimetatakse asümptootiliselt statsionaarseks e. paraboolseks mudeliks

  2. k < 0, R = (3 * k) / (8 * pii * G * roo_0) = R_max

    Näeme, et sellise Universumi paisumine kestab seni, kuni mastaabikordaja R omandab maksimaalse väärtuse. Hiljem saab R' negatiivseks, paisumine asendub kokkutõmbumisega, mis kestab seni, kuni R saab nulliks. Siis meie funktsioon katkeb.

    Jääb veel kolmas võimalus:

  3. Kui k > 0, ei peatu paisumine kunagi.

Paistab, et saadud tulemus pole suurem asi. Kogu maailma saatus sõltub tühipaljast integreerimiskonstandist, mis teadupoolest võib omada suvalist väärtust.

Matemaatikas küll, mitte aga füüsikas. Tegelikult meie maailm eksisteerib üsna kindlal kujul ja seetõttu on ka meie integreerimiskonstandil looduse poolt antud väärtus olemas. Me teame mastaapkordaja tuletist R' (paisumiskiirust), kui õnnestuks vaatluste abil määrata ka teist jätku tuletis, saaks nende abiga leida ka integreerimiskonstandi k väärtuse.

Leitud "Universumi valem" pole füüsika seisukohalt muud kui energia jäävuse seadus. Võrrandi vasak pool -- v2 -- määrab laialilendavate galaktikate kineetilise energia. Parem pool, kus sees gravitatsioonikonstant, on aga kõigi galaktikate vastastikuse külgetõmbe potentsiaalne energia. Konstant näitab, kumb neist on suurem. Kui k = 0, on nad ühesuurused. Kui k > 0, on kineetiline energia suurem. Kui k < 0, on ülekaal potentsiaalsel energial. Siis peatab gravitatsioon paisumise ning "maailm kukub kokku".

Ja veel näeme, et kosmoloogiline printsiip on rikutud, vähemalt tema ajalises mõttes. Enne, kui seda arutada, vaatame ka kolmandat mudelit.

Täiendav tekst:
Milne'i mudel

3. Relativistlik mudel (A. Einstein 1916, A. Friedmann 1922 [W. de Sitter 1917, Heckmann, G. Lemaitre...]). Mudel järeldub vahetult A. Einsteini üldrelatiivsusteooria võrranditest. Kui pöörata tähelepanu aastaarvudele, näeme, et see mudel oli ajalooliselt esimene. Veelgi enam, ta viidi "katuse alla" juba enne Hubble'i seaduse avastamist.

Üldrelatiivsusteooria, tänapäeva populaarseim gravitatsiooniteooria, ei kuulu koolifüüsika programmi. Põhjuseks on ülikeeruline matemaatika ning suhteliselt väikesed (kui mitte öelda olematud) rakendamise võimalused. Et saada Einsteini võrrandi lahendit "kogu Universumi kohta" tuleb analoogiliselt eelmise punktiga kirja panna võrrandid mingi galaktika kohta ja esitada lahend mastaapkordaja kaudu. 1917. a., kui Hubble'i seadust polnud veel avastatud, häiris uurijaid kõige rohkem püsiva ajas muutumatu lahendi puudumine. Et sellest vastuolust vabaneda, lisas Einstein võrrandeisse nn. kosmoloogilise liikme, mis suurtes mastaapides raskusjõu tasakaalustas, muutes lahendi vastavaks kosmoloogilise printsiibi nõuetele. Alles 1922. a. söandas A. Friedmann välja tuua ka mittestatsionaarse lahendi, mis ongi kaasaegse füüsikalise kosmoloogia alus.

Täiendav tekst:
Üldrelatiivsusteooria elemente

<--- --->

[Joonis 1]
Joonis 1. Galaktikate vahelise kauguse kasv paisuval sfääril.

[Joonis 2]
Joonis 2. Milne'i mudeli võimalikud evolutsiooniteed.

[ Peatüki indeks | Õpiku tekst | Illustratsioonid | Viited | Kordamisküsimused ]

Õpiku tegijad / opik@obs.ee
© Tartu Tähetorni Astronoomiaring 1997-99

14. märts 1999

 [Avatud Eesti Fond]

Selle õpiku valmimist on toetanud Avatud Eesti Fond.