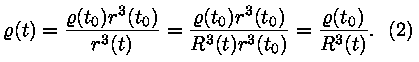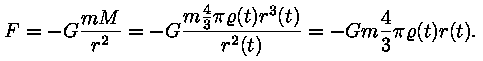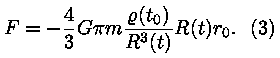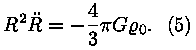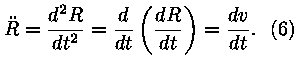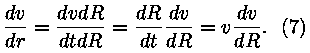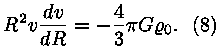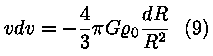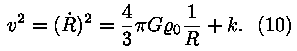Milne'i mudel
JAAK JAANISTE
Olgu meil paisuv kera. Selle kera suvalise punkti asukoha saame
anda kohavektori 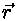 abil. Kui see kera paisub
ühtlaselt, võime kohavektori (ja koos temaga suvalise vektori
selles keras) kirja panna kujul abil. Kui see kera paisub
ühtlaselt, võime kohavektori (ja koos temaga suvalise vektori
selles keras) kirja panna kujul
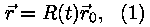 kus R(t) on suvaline ajast sõltuv funktsioon,
kus R(t) on suvaline ajast sõltuv funktsioon,
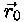 aga
meid huvitava punkti kohavektor hetkel t0, mida loeme
vaatlushetkeks. Tasub meeles pidada, et R(t0) =
1, vt. valem (1). aga
meid huvitava punkti kohavektor hetkel t0, mida loeme
vaatlushetkeks. Tasub meeles pidada, et R(t0) =
1, vt. valem (1).
Ainetiheduse 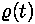 leiame valemist leiame valemist
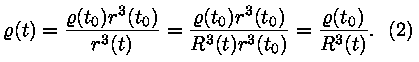
Leiame nüüd mingi galaktika liikumisvõrrandi. Newtoni II
seaduse järgi on tema kiirendus a = F / m, temale
mõjuva jõu leiame gravitatsiooniseadusest:
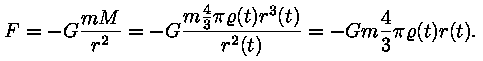
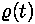 asendame valemist (2): asendame valemist (2):
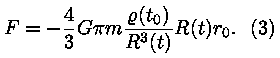 Viimast saab taandada R(t)-ga; F asendame Newtoni II
seadusest
Viimast saab taandada R(t)-ga; F asendame Newtoni II
seadusest
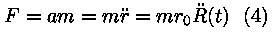 ja korrutame mõlemaid pooli R2-ga. Kui
nüüd jagada mõlemat poolt korrutisega
ja korrutame mõlemaid pooli R2-ga. Kui
nüüd jagada mõlemat poolt korrutisega 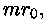 saame diferentsiaalvõrrandi, millest on kadunud nii
proovikeha kohavektor kui tema mass: saame diferentsiaalvõrrandi, millest on kadunud nii
proovikeha kohavektor kui tema mass:
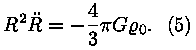 Ja ongi meie nipitamine läbi -- meil on võrrand, mis kirjeldab
paisumisteguri -- mastaabikordaja sõltuvust
ajast, kusjuures võrrandi ainsad parameetrid on keskmine
ainetihedus ning gravitatsioonikonstant. Kui meil õnnestub see
võrrand lahendada -- ja miks ta ei peaks õnnestuma -- ongi
käes valem Universumi paisumise kohta. Teades mastaabikordaja
sõltuvust ajast, saame kergesti leida suvalise kauguse ajalise
muutumise, kasvõi lõpmatuseni välja.
Ja ongi meie nipitamine läbi -- meil on võrrand, mis kirjeldab
paisumisteguri -- mastaabikordaja sõltuvust
ajast, kusjuures võrrandi ainsad parameetrid on keskmine
ainetihedus ning gravitatsioonikonstant. Kui meil õnnestub see
võrrand lahendada -- ja miks ta ei peaks õnnestuma -- ongi
käes valem Universumi paisumise kohta. Teades mastaabikordaja
sõltuvust ajast, saame kergesti leida suvalise kauguse ajalise
muutumise, kasvõi lõpmatuseni välja.
Võrrand, mis meil ees, on Newtoni dünaamika
tüüpvõrrand. Aga ta on teist järku
diferentsiaalvõrrand, ja seda me lahendada ei oska. Tuleb veel
nipitada. Alustame sellest, et kirjutame tuletised ümber Leibnitzi
sümboolikasse:
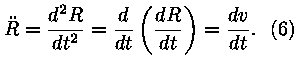 Siin v on muidugi kiirus, aga sellega me veel ei lõpeta.
Korrutame ja jagame saadud avaldist dR-ga:
Siin v on muidugi kiirus, aga sellega me veel ei lõpeta.
Korrutame ja jagame saadud avaldist dR-ga:
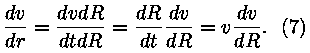
Nagu näeme, on nüüd võrrandist kadunud ka aeg.
v(t) on kiirus ainult näiliselt, tegelikult on see
mastaabikordaja tuletis aja järgi, mis näitab paisumiskiirust,
st. paisuva ruumi objektide (galaktikate) suhtelist kaugenemist
ajaühiku kohta. See ei ole Hubble'i konstant, mis on ka
paisumiskiirus, aga pikkusühiku kohta, ehk teiste
sõnadega paisumiskiiruse ja mastaabikordaja suhe 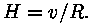
Võttes kokku võrrandid (5), (6) ja (7),
saame lihtsa diferentsiaalvõrrandi:
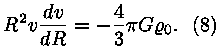 Eraldame muutujad:
Eraldame muutujad:
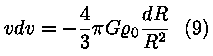 ning integreerime:
ning integreerime:
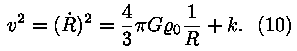 Saimegi kätte valemi, mis kirjeldab "kogu maailma" arengut.
Kasutatud matemaatilise võtte sisu seisneski selles, et viia
kauguste muutumise valem üle suhtelise pikenemise valemiks.
Nüüd võivad kaugused olla ükskõik millised,
meie valem kehtib nende kõigi kohta. Seega kogu Universumi kohta.
Saimegi kätte valemi, mis kirjeldab "kogu maailma" arengut.
Kasutatud matemaatilise võtte sisu seisneski selles, et viia
kauguste muutumise valem üle suhtelise pikenemise valemiks.
Nüüd võivad kaugused olla ükskõik millised,
meie valem kehtib nende kõigi kohta. Seega kogu Universumi kohta.
Kaval mõte, kas pole?
|