Kosmoloogia - 5. osa: Universum

[ Peatüki indeks | Õpiku tekst | Illustratsioonid | Viited | Kordamisküsimused ]

4. peatükk: Kosmoloogilised mudelid

Üldrelatiivsusteooria elemente

JAAK JAANISTE

Üldrelatiivsusteooria lõi Albert Einstein koostöös M. Grossmanniga 1910-1916 jätkuna 1905. a. valminud erirelatiivsusteooriale. Üldrelatiivsusteooria aluseks on ekvivalentsusprintsiip:

Raske (graviteeruv) mass ja inertne mass on ekvivalentsed; pole mingit võimalust kindlaks teha, kas vaadeldav keha asub gravitatsiooniväljas või kiirendusega liikuvas taustsüsteemis.

Nagu teada üldtuntud legendist, tuletas 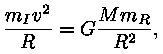I. Newton oma gravitatsiooniseaduse kahe keha -- puu otsast kukkuva õuna ja taevast mitte kukkuva Kuu võrdlemisest. Kuu püsimise orbiidil kindlustab gravitatsioonijõu ja tsentrifugaaljõu võrdsus:

m_I * v^2 / R = G * (M * m_R / R^2),
kukkuva õuna liikumise aga Newtoni II seadus:
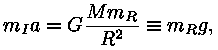
m_I * a = G * (M * m_R / R^2 = m_R * g,
kus g = G * M_Maa / (R_Maa)^2 = 9,8 m/s^2 on raskuskiirendus Maa pinnal. Kui me nüüd neis võrrandites massi (ükskõik, kas Kuu või õuna oma) maha tõmbame, siis olemegi rakendanud ekvivalentsusprintsiipi -- oletanud, et raske mass mR ja inertne mass mI on alati võrdsed. Muidugi on neid valemeid võimalik kontrollida ja sedagi on tehtud. Tulemus näitab, et tänapäeva mõõtmistäpsuse juures mingit mõõdetavat erinevust neil kahel massil ei ole. Ehk, veel täpsemalt
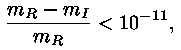
m_R - m_I / m_R < 10^(-11),
just nii kaugele on tänaseks jõutud nende võrdsuse täpse määramisega.

Ekvivalentsusprintsiibi ilminguks on kaaluta olek langevas liftis või ümber Maa tiirlevas kosmoselaevas -- mitte kummaski pole mitte mingite mõõtmistega võimalik kindlaks teha ei kiirenduse ega gravitatsioonivälja olemasolu.

Kuidas seda matemaatiliselt väljendada, selles on küsimus. Einstein jt. lahendasid selle oletusega kõverast ruumist. Idee on iseenesest lihtne: kosmoselaeva orbiit tasases (eukleidilises) ruumis on ekvivalentne sirgega (nimetame seda geodeetiliseks jooneks) kõveras ruumis. See tähendab, et ruum peab olema nii kõver, et kõver trajektoor oleks temas sirge; sirge all mõistetakse, nagu tavaliseski ruumis, lühimat teed kahe punkti vahel. (Et segadust vältida, on tema nimeks "geodeetiline joon".) Kõverate ruumide geomeetria (see ongi see keeruline matemaatika) töötasid välja N. Lobats^evski (negatiivse kõverusega nn. hüperboolsed ruumid, 1826) ja B. Riemann (suvalise kõverusega ruumid, 1854); Einsteinil jäi üle vaid siduda ruumi kõverus massi ja liikumist kirjeldavate suurustega. Tulemuseks on nn. Einsteini võrrand(ite süsteem), mille lahendamisel saadakse proovikeha (Kuu, õun) "maailmajoon" ülejäänud kehade (masside) poolt määratud kõveras ruumis.

Enne, kui sulgeme kasti, püüame seda uut sõna veel pisut selgitada. Juba erirelatiivsusteooria kasutab neljamõõtmelist koordinaatsüsteemi, kus lisaks kolmele ruumiteljele on olemas veel ajatelg. Et mõõtühikud peavad kõigil telgedel olema samad, tuleb ajamomenti enne teljele kandmist korrutada valguse kiirusega, mis erirelatiivsusteooria järgi on kõigis taustsüsteemides ühesugune. Nii saamegi neli koordinaati: x, y, z ja ct; keha liikumisteele (punktide hulk, kus liikuv keha asub erinevatel ajamomentidel) vastabki neliruumis tema maailmajoon.

Joonis. Liikuva keha kahemõõtmeline trajektoor tasandil xy ja tema maailmajoon ruumis x, y, ct.

[ Peatüki indeks | Õpiku tekst | Illustratsioonid | Viited | Kordamisküsimused ]

Õpiku tegijad / opik@obs.ee
© Tartu Tähetorni Astronoomiaring 1997-98

14. märts 1998

 [Avatud Eesti Fond]

Selle õpiku valmimist on toetanud Avatud Eesti Fond.