Kosmoloogia - Einsteini-Friedmanni kosmoloogia: Õpiku tekst

5. osa: Universum

[ Peatüki indeks | Õpiku tekst | Illustratsioonid | Viited | Kordamisküsimused ]

5. peatükk: Einsteini-Friedmanni kosmoloogia

Friedmanni lahendi järgi kujutab ruumi paisumist (mastaapkordaja muutust) kõver, mis sõltuvalt parameetri 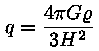väärtusest on kas hüperbool (q < 0,5), parabool (q = 0,5) või ellips (q > 0,5). Nagu Milne'i mudelis, vastab ka siin kahele esimesele lõpmatult paisuv ruum, kolmandas kestab paisumine mingi ajahetkeni t_m (vastab mastaapkordaja maksimaalväärtusele R_m), mille järel algab kokkutõmbumine. Kõik nagu eelmises punktis, kuid ühe erinevusega. Selleks on kõver ruum.
Kõver ruum. Einsteini järgi on tasane ainult tühi ruum. Igasugune ruum, kus on kasvõi kübegi ainet, peab olema kõver, ja see kõverus on igal juhul positiivne.
Mida see tähendab? Aga seda, et niisugustes ruumides ei kehti Eukleidese geomeetria viies aksioom:
Läbi sirgel mitte asuva punkti saab panna ühe ja ainult ühe antud sirgega paralleelse sirge.

Aksioomi saab rikkuda kahel viisil: lubades panna läbi punkti kuitahes palju paralleelseid sirgeid või siis keelates sellise sirge panemise üldse. Esimesel juhul saame negatiivse, teisel positiivse kõverusega ruumi.
Meie kujutlusvõime on seotud tavalise kolmemõõtmelise ruumi ja Eukleidilise geomeetriaga. Seepärast ei suuda me ette kujutada kõveraid või kõrgema dimensiooniga ruume. Küll aga võime ette kujutada erineva kõverusega pindu tavalises ruumis. Negatiivse kõverusega on näiteks sadul. Kuidas seal paralleelseid sirgeid konstrueerida ja palju neid mahub läbima üht punkti, on meie jaoks pisut keeruline ülesanne. Me ei oska diferentsiaalgeomeetriat, ja kui ka oskaksime, oleks ikkagi sellega tükk tegemist. Hoopis lihtsam on hakkama saada positiivse kõverusega pinnaga, milleks on kolmruumis ellipsoid ja kõik tema sugulased. Kõige lihtsam neist on kerapind -- sfäär. Sirgeks sfääril on nn. suurringid -- jooned, mis tekivad sfääri lõikamisel tema keskpunkti läbiva tasandiga. Joonistame gloobusele ühe sellise ringi, võtame selle kõrval punkti ja püüame sellest läbi panna eelmisega paralleelset suurringi. Näeme, et see ei õnnestu: ringid kas lõikuvad (nagu meridiaanid) või on küll paralleelsed (paralleelid), kuid suurring on neist ainult üks -- ekvaator. Seega positiivse kõverusega pinnal paralleelseid sirgeid ei ole, samuti pole neid ka positiivse kõverusega ruumis.
Kõne all oleval ruumil on veel üks omadus: ta suurendab kõigi eemal olevate esemete mõõtmeid. Võrrelge gloobusel kahe meridiaani vahekaugust samasuguse tipunurgaga tasanurga haarade kaugusega ja te näete, et punktid kera pinnal asuvad üksteisele alati lähemal kui tasandi punktid. See tähendab. et vaadates taevalaotusse kõveras ruumis, näeme seda veelgi tühjemana. Tõsi küll, galaktikad ise paistavad jälle suuremana...
Kõige tähtsam positiivse kõverusega ruumi omadus on aga see, et tema ruumala on lõplik. Täpselt nagu sfääri pindalagi. Seega on meie maailmal olemas nii lõplik ruumala kui ka lõplik mass.
Horisont. Kahjuks ei saa me neid numbreid ütelda. Me ei tea neid, kuna me ei näe mitte kogu Universumit, vaid ainult osa sellest. Põhjuseks on valguse kiiruse lõplikkus. Maksimaalne kaugus, kuhu meie "silm ulatub", on 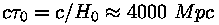-- kaugus, kust valgus on parasjagu meieni jõudnud.
Seistes kera pinnal, ei näe me samuti kogu kera, vaid ainult vahemaad iseendast kuni horisondini -- piirini, kus vaatekiirtest moodustuv koonus ühtib kera pinnaga (puutub kera pinda). Sama lugu on Universumiga: pilt lõpeb seal, kus 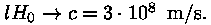Aga siingi on vaatamata näilikule analoogiale sügav erinevus. Kui maapealne horisont paistab vaatlejale terava joonena (kõik maapinnal nähtavad esemed, vaatamata nende tegelikule kaugusele, rivistuvad ühele joonele -- silmapiirile), siis kosmoloogilise horisondiga on lugu teine. Eemaldumiskiiruse lähenemisel valguse kiirusele kasvab punanihe (muidugi relativistlike valemite kohaselt) lõpmata suureks, mis loob vaatlejale illusiooni tohutu suurest, kuid tühjast ruumist.
See, kui suurt osa Universumist me näeme, sõltub nii mudeli arengut kujutavast kõverast (joon.*** lk ***) kui meie (st. vaatleja) asukohast sellel. "Kogu Universum" on näha vaid siis, kui Hubble'i aeg 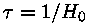on lõpmata suur, st. alates hetkest, kus paisumine on peatunud, mis on võimalik üksnes kinnise mudeli puhul. Et meie Universum praegu paisub (ja üsna suure kiirusega) on see meie jaoks kauge tuleviku võimalus. Kui üldse.
Kas kõveras ruumis saab näha iseenda selga? Põhimõtteliselt jah, kui kõverus on piisavalt suur, st. ruum piisavalt väike. Universumis paraku mitte, ja seda valguse kiiruse lõplikkuse tõttu. Meie seljalt peegeldunud kiir jõuaks meie silmadeni võib-olla mitmesaja miljardi aasta pärast, ja sedagi vaid juhul, kui ruum ei paisuks. On karta, et selle aja peale pole enam silmi, mis sündmuse fikseeriks. Ega ka Maad, Päikest ja võib-olla kogu Universumit.
Asi, mida me aga kindlasti uurida saame, on Universumi minevik. Maailmal tundub olevat "üsna hea mälu", mistõttu pilt möödanikust saab küllaltki detailiderohke.
Ruumala ja tihedus. Vaatame veel kord joonist **. Mastaapkordaja lähenemine nullile mingil "alghetkel" t = 0 tähendab, et kõik kaugused olid sel ajahetkel nullid. Koos kaugustega peaks nulliks saama ka Universumi ruumala -- ning loomulikult ka horisont. Kui jääda kindlaks põhimõttele, et aine jäävuse seadus kehtib, tähendab see samaaegselt lõpmatut tihedust.
Seda algseisundit nimetatakse mudeli singulaarsuseks. Matemaatikas tähendab singulaarsus funktsiooni katkevust teatud argumendi väärtusel. Võiks öelda, et meie Universumi (paisumise) valemis on määramispiirkond piiratud ajatetkega t = 0.
Vanus. Et seda mõistet selgitada, peame mastaapkordaja käiku kujutava joonise pisut ümber tegema, viies vaatlushetke t₀ = 0. Universumi minevikule vastab siis negatiivne aeg (nagu meie ajaarvamises aastad enne Kristust), tulevikule aga positiivne aeg. Universumi vanuseks loeme nullpunktist mudeli singulaarsuseni möödunud aja. Et kõik mudelid peavad vaatlushetkel klappima vaadeldava paisumiskiirusega, on neil hetkele t = 0 vastavas punktis R(t=0) = 1 ühine puutuja, mis lõikub ajateljega punktis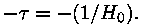
Jooniselt näeme, et mudeli vanus on seda suurem, mida väiksem on kiirendusparametri väärtus. Kinnised mudelid on üldiselt väga noored, vanusega alla kümne miljardi aasta. Lahtised mudelid tulevad vanemad, jäädes siiski alla Hubble'i ajale (13 miljardit aastat). Nii või teisiti, kui neid aegu võrrelda kasvõi Maa vanusega (ligi 5 miljardit aastat), siis polegi meie Universum kes-teab-kui-vana. Tuleb muidugi arvestada, et aeg ei ole relatiivsusteoorias mingi absoluut. See, millest praegu jutt, on "kaasaliikuva vaatleja aeg", st. aeg, mida tajub paisuva Universumi mingis galaktikas olev ja sellega koos liikuv vaatleja. Vanajumalal, kes asja kõrvalt vaatab, võib sootuks teine ajaarvamine olla.
Temperatuur. Enne, kui numbrite juurde asuda, tasuks siingi mõisted täpsemalt paika panna.
Termodünaamikas (** kl.) kasutatud temperatuur on kineetiline temperatuur ja see on määratud aine osakeste -- molekulide -- kaootilise liikumise kiirustega (täpsemalt, molekulide keskmise kineetilise energiaga). Tasakaalus süsteemi jaoks vastab molekulide kiiruste jaotus Maxwelli valemile ja osakeste keskmine kineetiline energia on
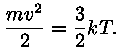See temperatuur on niisiis võrdeline kineetilise energiaga.
Optikas, täpsemalt kiirgus- e. kvantoptikas, määrab temperatuuri tasakaalulise kiirguse kvandi tõenäoseim energia. Tasakaalulise kiirguse energiajaotust (spektrit) kirjeldab Planck'i valem (musta keha kiirguse spekter) ja seose temperatuuriga saame Wieni nihke seadusest 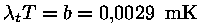( 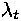on Planck'i kõvera maksimumile vastav lainepikkus. Eelpoolöeldust peaks selge olema, et kineetilise temperatuuri mõõtmine Universumis ei tule kõne alla. Jääb üle otsida tasakaalulist kiirgust, mis oleks täielikult isotroopne, st. tuleks vaatlejani ühtviisi kõigist suundadest (sellist kiirgust nimetatakse foonkiirguseks) ja millel on musta keha kiirguse spekter.
Selline kiirgus avastati 1965. a. ja tema spektri maksimum asub lainepikkusel 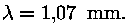Wien'i valemi järgi vastab sellele temperatuut 2,7 K (-270°C).
Kui kiirgus puuduks, oleks tegu külma, st. rõhuvaba mudeliga, kus toimib ainult gravitatsioon. Kiirgusfooni olemasolu näitab, et Universum on kunagi olnud soojusliikumises, millele vastava kiirguse temperatuur nüüd ruumi paisudes väheneb. Kui vaadata minevikku, siis pidi temperatuur olema seda kõrgem, mida väiksem oli mastaabikordaja. Et Universumi sünnihetkele vastab R(t) = 0, siis peab 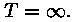Seda muidugi klassikalise füüsika seisukohalt.
Relativistliku mudeli alghetk, millele vastab suur tihedus, temperatuur ja paisumiskiirus, kannab astronoomide slängis nime Suur Pauk (ingl. Big Bang). Väljend, mida ei tasuks just täht-tähelt võtta.

Joonis 1. Kõvera ruumi geomeetria: seos vaatenurga ja kauguse vahel tasapinnal (A'B') ja sfääril (AB). Näeme, et A'B' > AB.

Joonis 2. "Osakese horisont" -- tähtedelt, mis asuvad meist kaugemal kui ( on Universumi vanus), pole valgus veel meieni jõudnud.

Joonis 3. Universumi areng ette antud Hubble'i konstandi H₀ jaoks kiirendusparameetri q₀ eri väärtuste korral.

Joonis 4. Kosmilise foonkiirguse spekter. Intensiivsuse maksimum lainepikkusel 1,1 mm vastab temperatuurile 2,7 K.

Foto 1. Kompanii "Bell Telephone" ruupor-antenn, millega foonkiirgus 1965. a. avastati.