Kosmoloogia - Maa: Veekera

1. osa: Maa ja taevas

[ Peatüki indeks | Õpiku tekst | Illustratsioonid | Viited | Kordamisküsimused ]

1. peatükk: Maa

Veekera
JAAK JAANISTE

Millise kuju peaks võtma pöörlev planeet? Ega me seda arvutada ei oska (ehkki tegu on klassikalise mehaanika ühe lemmikülesandega, mida on lahendatud ja lahendeid parandatud juba mitusada aastat). Aga püüame hästi lihtsate võtetega leida, millise tasakaalulise kuju peaks omandama ühtlase tihedusega vedelikust koosnev kera, kui see panna aeglaselt pöörlema. "Aeglaselt" tähendab näiteks üks tiir ööpäevas. Vedelikust räägime aga selle pärast, et veepind on teadupoolest alati risti raskusjõu suunaga. Kui kera ei pöörle, piirdubki kogu jõud gravitatsiooniga, mis on suunatud kera tsentrisse ja kera pind ongi ju risti raadiusega. Kui kera pöörleb, lisandub tsentrifugaaljõud ning pind deformeerub. Aga milliseks?
Vaatame ühtlase tihedusega kera, mille tihedus on 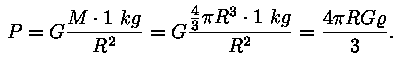, raadius R ja pöörlemisperiood T. Kera pinnal asuvale "veetükile" massiga 1 kg mõjub raskusjõud
P = (G * M * 1 kg) / R^2 = (G * 4/3 * pii * R^3 * 1 kg) / R^2 = (4
* pii * R * G * roo) / 3.
Tsentrifugaaljõud 1 kg kohta laiuskraadil :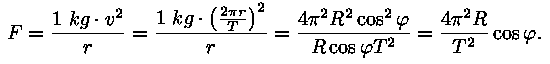
F = (1 kg * v^2) / r = (1 kg * (2 * pii * r / T)^2 ) / r
= (4 * pii^2 * R^2 * cos^2(fii) ) / (R * cos(fii)
* T^2) = ((4 * pii^2 * R) / T^2) * cos(fii).

Nagu me teame, on vee pind alati risti raskusjõu suunaga. Sellel surmkindlal faktil põhineb vesilood, mida ehitusmehed juba sadu aastaid kasutavad. Kui meil on tegu keraga, on gravitatsioonijõud suunatud kera tsentrisse -- seega piki raadiust, millega kera pind on alati risti. Pildi rikub pöörlemisel tekkiv tsentrifugaaljõud, mis pole suunatud piki raadiust, see-eest on aga alati risti pöörlemisteljega. Nagu jooniselt näha, pole nende jõudude summa enam raadiusesuunaline. Seega ei saa ka meie kera pind enam olla risti raadiusega. See tähendab, et pöörlev veekera polegi enam kera.
Katsume leida tekkiva keha valemi. Ilmselt on pilt telgsümmeetriline -- järelikult on tegu pöördkehaga. Vaatame, milline on selle keha telglõige. Aga kõigepealt arvutame raskusjõu suuna: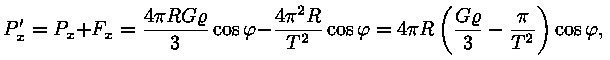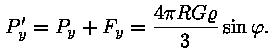
ehk koordinaatides P'_x = P_x + F_x = ((4 * pii * R * G * roo) /
3) * cos(fii) - ((4 * pii^2 * R) / T^2) * cos(fii) = 4 * pii * R * ((G *
roo) / 3 - pii / T^2) * cos(fii),
P'_y = P_y + F_y = ((4 * pii * R * G * roo) / 3) * sin(fii).
Et kirjut pilti loetavamaks muuta, tähistame kordaja mis määrab raskusjõu kerakujulise (mittepöörleva!) planeedi pinnal. Veekera normaali võrrandiks tuleb
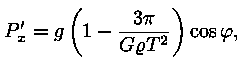
P'_x = g * (1- (3 * pii) / (G * roo * T^2)) *
cos(fii),

Et saada veepinna asendit -- meie veekera puutujat punktis M -- tuleb leida sirge, mis läbib punkti M ja on risti meie poolt leitud vektoriga. Suuna muutmine on lihtne: tuleb meie valemeis nurgale 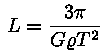liita täisnurk, ehk, teiste sõnadega, asendada siinus koosinusega ja ümberpöördult. Kordajate rehkendamine pole nii lihtne; jätame nad seekord rahule -- kel huvi, võib edasi uurida. Tulemuseks on valemid
,
, millele vastab ellips, kus b ja a on selle poolteljed ja L tähistab lapikust. Oma rehkendustega me leidsimegi just lapikuse; kui valemisse L = (3 * pii) / (G * roo * T^2) panna andmed Maa kohta ( = 5500, T = 24 h = 86400 s), saame tulemuseks L = 0,0034, mis üsna täpselt sobib tegeliku lapikusega (0,0035).
Niisiis omandab veekera pöörlemisel pöördellipsoidi e. sferoidi kuju. Ja seepärast ei ole tarvis imestada, miks ookeanide vesi poolustele ei valgu.
Küsin: Arvutage ka teiste planeetide lapikused, kasutades planeeditabelis toodud andmeid.