Kui kaugel on silmapiir?
JAAK JAANISTE
|
Näitame joonisel tükikest maakera. Silmapiiri moodustab vaatleja
V silmast maakerale tõmmatud puutuja. Loeme silma
kõrguseks maapinnast 170 cm, Maa aga ideaalseks keraks. Kerale
tõmmatud puutuja on on puutepunktis S risti kera raadiusega
R; vaatleja näeb kera pinnast seda osa, mis on talle
lähemal raadiusega l tõmmatud ringjoonest
(täpsemalt: moodustajaga l kujundatud koonuse
põhjast).
|
![[Joonis]](pildid/box1s.gif)
|
Täisnurksest kolmnurgast OSV
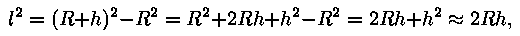 kuna
kuna
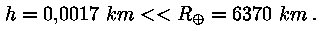
Kauguse l leidmiseks on nüüd lihtne valem:
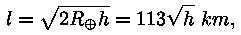 kui lähtuda Maa raadiusest
kui lähtuda Maa raadiusest
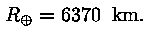 Pannes valemisse
Pannes valemisse
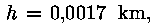 saame keskmise vaatleja horisondiks saame keskmise vaatleja horisondiks
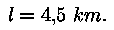
Muidugi, kui h on küllalt suur, hakkab valem streikima, sest
ärajäetud
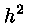 pole enam nii väike. Aga see
juhtub alles mitme tuhande kilomeetri kõrgusel... Õigem
oleks öelda, kaugusel, sest see tähendab juba vaadet kosmosest. pole enam nii väike. Aga see
juhtub alles mitme tuhande kilomeetri kõrgusel... Õigem
oleks öelda, kaugusel, sest see tähendab juba vaadet kosmosest.
Küsin: Leidke silmapiir Oleviste torni (127 m), Suure Munamäe
(koos torniga 342 m) ja Mt Everesti (8848 m) otsast vaadates.
|
