Relativistlik punanihe
JAAK JAANISTE
Kvasarite spektrid, kus hästituntud spektrijoonte lainepikkus on
kasvanud mitmekordseks, kutsub esile näiva vastuolu
relatiivsusteooria põhiprintsiibi - valguse kiiruse konstantsusega.
Tähendab ju meie poolt lk.** toodud valemi 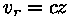 korral z > 1 valguse
kiirusest suuremat eemaldumiskiirust. korral z > 1 valguse
kiirusest suuremat eemaldumiskiirust.
Põhjuseks on asjaolu, et eemaldumiskiiruse rehkendamisel Doppleri
efektist kasutasime me tavalisi, Newtoni mehaanika valemeid. Kui tahame
leida lainepikkuse muutust (spektrijoone nihet) valguse kiirusele
lähedaste suhteliste kiiruste korral, peame kasutama
relatiivsusteooriat.
Lähtume erirelatiivsusteooria põhipostulaadist: valgus on
lainetus, mis levib kõigis inertsiaalsüsteemides
ühesuguse kiirusega c. Kui mingi valgusallikas kiirgab
lainepikkusel 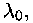 peab ta võnkuma sagedusega peab ta võnkuma sagedusega
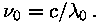 Sellise laine võrrandiks
on Sellise laine võrrandiks
on
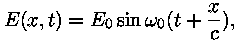 kus
kus 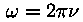 on nn. ringsagedus. See, nagu
iga teinegi füüsika võrrand, peab kehtima
sõltumatult inertsiaalsüsteemist, milles me lainet (st.
valgust) vaatleme. on nn. ringsagedus. See, nagu
iga teinegi füüsika võrrand, peab kehtima
sõltumatult inertsiaalsüsteemist, milles me lainet (st.
valgust) vaatleme.
Kujutame nüüd, et valgusallikas eemaldub meist relativistliku,
valguse kiirusele c lähedase kiirusega. Vastavalt
relatiivsusteooriale erinevad valgusallikaga seotud
inertsiaalsüsteemis kehtiv aeg ja pikkus meie, st. vaatleja omast.
Tähistades neid vastavalt t' ja x', tuleb meil
üleminekuks vaatleja paigalseisvasse süsteemi kasutada Lorentzi
teisenduse valemeid (A. Ainsaare õpiku lk.
13):
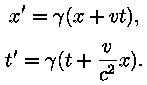
Vaatame, kuidas teiseneb lainevõrrandi liige 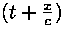 üleminekul üleminekul 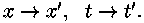 Saame: Saame:
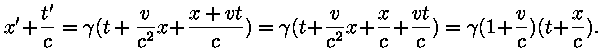
Nüüd tuleb natuke rehkendamist. Meenutame, et kinemaatiline tegur
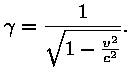 Lugejasse tuleva
Lugejasse tuleva 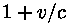 võime kirjutada võime kirjutada 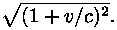 Nimetajas ruutjuure all olev avaldis
teisendub Nimetajas ruutjuure all olev avaldis
teisendub 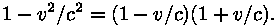 Kui viia avaldise esimene pool ühise ruutjuure alla, saab
Kui viia avaldise esimene pool ühise ruutjuure alla, saab 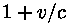 maha taandada. Järele jääb maha taandada. Järele jääb
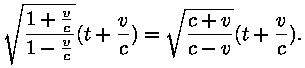
Et lainevõrrand kehtiks ka vaatleja süsteemis, peab sagedus
muutuma:
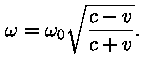
Pilt on sama, mis Doppleri efekti korral -- eemalduva allika jaoks sagedus
väheneb (lainepikkus kasvab), läheneva allika korral vastupidi.
Muutunud on valem: varasema 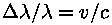 asemel
on märksa keerulisem avaldis. Püüdke see tuletada ja leida
ka valem eemaldumiskiiruse v leidmiseks asemel
on märksa keerulisem avaldis. Püüdke see tuletada ja leida
ka valem eemaldumiskiiruse v leidmiseks 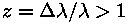 korral. korral.
Kas saite hakkama? Valemid on:
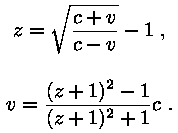
|
![[joonis]](pildid/rel-pnn-k.jpg)
Joonis. Punanihke z sõltuvus eemaldumiskiirusest v
relativistlikul juhul.
|
Leitud kiirusest võiks põhimõtteliselt arvutada
kvasari kauguse. Paraku pole see kaugus õige. Sest ilmaruum pole
neil kaugustel enam tavaline, vaid kõver. Ja pealegi paisuv. Aga
nende asjadega tegeleb juba päris-kosmoloogia.
|
