Kosmoloogia - Tähtede füüsika: Tähe tasakaaluvõrrand

3. osa: Tähed

[ Peatüki indeks | Õpiku tekst | Illustratsioonid | Viited | Kordamisküsimused ]

5. peatükk: Tähtede füüsika

Tähe tasakaaluvõrrand - "tähemudel"
JAAK JAANISTE

Alustati võrrandist, mille liikmeteks on tähe mass, kiirgusvõime, läbimõõt, temperatuur ja keemiline koostis. Need andmed võis võtta vaatlustest, aga ka arvutada tasakaaluvõrrandi abil. Et tähti oli vaadeldud palju, sai erinevaid mudeleid omavahel võrrelda, välja selgitada sarnaseid jooni ning põhjendada erinevusi. Loodus andis uurijatele äärmiselt huvitava ning hästi piiritletud ülesande, mille lahendamine selle sajandi kolmekümnendatel aastatel meenutas mingit ülemaailmset olümpiaadi.
Lähte-eeldused on lihtsad; täht on üldse kõige lihtsama füüsikaga keha terves maailmas. Ta kujutab endast peaaegu ideaalsest gaasist kera, mida hoiab koos gaasi enda gravitatsiooniväli. Ainsaks jõuks, mis raskusjõudu tasakaalustades hoiab tähte kokku langemast, on gaasi rõhk, mis sõltub tihedusest ja temperatuurist vastavalt ideaalse gaasi olekuvõrrandile:
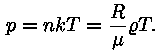p = n * k * T = (R / müü) * roo * T. NB! Mitte segi ajada gaasikonstanti R ja Päikese raadiust !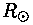
Täheks, mida modelleerida, valime Päikese kui kõige paremini tuntud ja samal ajal meile kõige olulisema tähe. Rõhu Päikese sisemuses määrab vaatluse all olevast punktist pinnani ulatuva gaasisamba kaal. Kui võtta samba ristlõige võrdseks pinnaühikuga (ruutmeeter), on tsentrini ulatuva samba korral selle mass 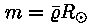( 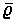on keskmine tihedus) ja rõhk tsentris
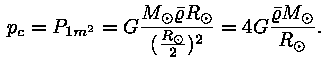p_c = P_(1m^2) = G * ((M_opunkt * roo_keskm *
R_opunkt) / (R_opunkt / 2)^2) = 4 * G * (roo_keskm * M_opunkt) /
R_opunkt. Et raskusjõu väljas rõhk tsentri suunas kasvab, peavad tasakaaluolekus kasvama ka tihedus ja temperatuur; tiheduse käik omakorda määrab gravitatsioonivälja tugevuse. Selle äärmiselt huvitava probleemi lahendas R. Emden 1907. a.
Kuna gravitatsioonivälja tugevus tähe sisemuses sõltub aine tihedusest, on Emdeni mudel määratud gaasi rõhu ja tiheduse vahelise sõltuvusega. Kui lugeda temperatuur konstantseks, saame gaasi olekuvõrrandist 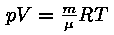rõhu avaldisek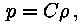s kus 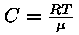ning 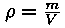tihedus. Niisugust mudelit nimetame isotermiliseks. Meie tasakaaluvõrrandist tuleb temperatuur Päikese keskmes
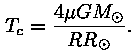
T_c = (4 * müü * G * M_opunkt) / (R * R_opunkt).
Pannes valemeisse Päikese massi 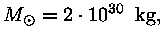raadiuse 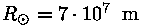ning keskmise 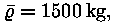tiheduse saame siit leida rõhu ja temperatuuri Päikese keskmes. Arvutage! Ehk suudate leida ka tiheduse?
Tavaliselt antakse tähemudelis rõhu ja tiheduse vaheline seos valemiga 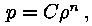nimetatakse selliseid mudeleid polütroopseiks. Et olekuvõrrand peab ikkagi kehtima, määrab polütroobi astendaja n temperatuuri sõltuvuse rõhust tähe sisemuses.
Kui püüaksime nüüd rehkendada Päikese tasakaaluolekut konstantsel temperatuuril 6000 kraadi (pinna temperatuur), saaksime tegelikust palju kordi suurema massi (tiheduse). Et seda ei juhtuks, tuleb astendaja polütroobi võrrandis võtta suurem. Arvutused näitavad, et Päikese keskmise tihedusega sobib kõige paremini astendaja n = 3 (isotermilise jaotuse 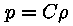korral oli see võrdne ühega), mis annab tiheduseks tsentris 76 500 kg/m³. Sel juhul on keskmine tihedus 1410 kg/m³, kui tihedus pinnal võtta nulliks. Temperatuurid leiame olekuvõrrandi abiga, Päikese jaoks on temperatuur tsentris 2 * 10⁷ K.
Nagu näeme, erineb viimane kaunis vähe meie poolt arvutatust. Rõhu ja tihedusega on lood kurvemad -- aga ega neid täpseid mudeleid ilmaasjata tehtud!
Esimese korrektse tähemudeli arvutas R. Emden 1907. aastal. 1926. a. täiendas A. Eddington tasakaaluvõrrandit kiirgusrõhku väljendava liikmega. Et temperatuur tsentris on suurem kui pinnal, peab toimuma energia voolamine sisemusest väljapoole. Nagu igapäevaelus, võib ka tähtedes soojusülekanne toimuda soojusjuhtivuse, kiirguse või konvektsiooni teel. Tänapäeva tähemudelid arvestavad neid kõiki. Eddingtoni mudel kujutas endast tähe tasakaaluolekut, kus sisemistes kihtides kiirgunud valgus neeldus välimistes kihtides, sealt kiirgunud valgus omakorda veel väljaspool ja nii edasi kuni pinnani. Et iga neeldumisega kaasneb ka impulsi ülekanne (tekib valgusrõhk), lisandubki tasakaaluvõrrandisse veel üks liige.

Joonis. Temperatuuri (a), rõhu (b) ja tiheduse (c) käik Päikese sisemuses. Tänapäeva mudel.