Kosmoloogia - 3. osa: Tähed

[ Peatüki indeks | Õpiku tekst | Illustratsioonid | Viited | Kordamisküsimused ]

2. peatükk: Tähtede vaadeldavad parameetrid

Tähesuuruste tähendusest

JAAK JAANISTE

[Joonis 1]
Joonis 1. Näivad tähesuurused -- Suur Vanker.

Tähe heledus on üks neist paljudest looduslike objektide omadustest, mida inimene on harjunud hindama oma meeleelundite -- antud juhul silma -- järgi. Lihtne on öelda, et üks täht on teisest heledam või tuhmim, aga kui palju, sellele on märksa raskem vastata. Tähekaartide joonistamisel tähistati heledamaid tähti lihtsalt suuremate märkidega, siit ka nimetus "tähesuurus" (magnitude).

Tänapäeva tähesuuruste skaala põhineb antiikajast pärit suurusjärkudel ning sajandivahetusel alustatud täppismõõtmistel. Erilise seadme -- fotomeetri -- abil saab määrata tähe poolt Maal põhjustatud valgustatust E (seesama, mis optika fotomeetria osas). Tähesuuruse arvutame nüüd Pogsoni valemiga

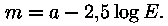
m = a - 2,5 * log (E).

See valem on kompromiss ajalooliste tähekaartide-kataloogide ning täppismõõtmiste vahel. Olgu meil näiteks kaks tähte, mille heledus erineb ühe tähesuuruse võra. Fotomeetrias tähendaks see

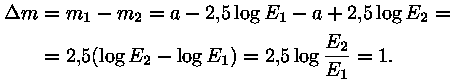
delta m = m_1 - m_2 = a - 2,5 * log (E_1) - a + 2,5 * log (E_2) = 2,5 * (log (E_2) - log (E_1) = 2,5 * log (E_2 / E_1) = 1.

Arvutame siit valgustatuste suhte 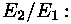E_2 / E_1 :

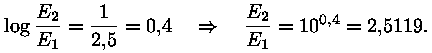
log (E_2 / E_1) = 1 / 2,5 = 0,4 --> E_2 / E_1 = 10^(0,4) = 2,5119.

Näeme, et kui esimesel tähel on ühe võrra suurem tähesuurus m1, siis on hoopis teine täht esimesest 2,5119 korda heledam. Et Pogsoni valemit tööle panna, peame veel teadma konstanti a. Selle määramiseks tuleb kokku leppida mingi taevatähe tähesuurus, edasi saab kõigi ülejäänute omad leida fotomeetriliste mõõtmiste (heleduste võrdlemise) abil. Eriti mugav on võtta etalontäheks täht, mille tähesuurus oleks null; siis oleks Pogsoni valemi järgi 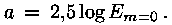a = 2,5 * log (E_(m=0)). Selliseks täheks on valitud Veega. Muidugi ei piirdu heledusstandard ühe tähega, vaid sisaldab hulka standardtähti erinevates taevapiirkondades.

[Joonis 2]
Joonis 2. Luik: näivad ja absoluutsed tähesuurused.

Veegast heledamatele tähtedele annab Pogsoni valem negatiivse tähesuuruse (Arktuurus -0,04; Siirius -1,44). Heleduse sõltuvus mõõteriista spektraaltundlikkusest lahendatakse nii, et ühele tähele antakse mitu tähesuurust. Esimene, silmaga määratud tähesuurus, kannab nime visuaalne (mv), lisanduvad fotograafiline (mpg), bolomeetriline (mb, määratud soojusliku toimega vastuvõtja abil) ning rida erinevate filtritega fotomeetrilisi tähesuurusi (U, B, V jt.)

Kui on teada tähe kaugus, saame määrata ka tema absoluutse tähesuuruse. Selleks kasutame valemit:

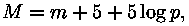M = m + 5 + 5 * log (p),
kus p on tähe aastaparallaks (tipunurk täisnurkses kolmnurgas, mille täisnurgale vastavas tipus asub Päike, teistes aga Maa ja vaadeldav täht). Parallaksi mõõdame kaaresekundites, ühele kaaresekundile vastab kaugus 1 parsek (pc), 0,1 kaaresekundile aga 10 pc.

Nii. Ja nüüd küsime: kust tulevad valemisse kordaja 5 ning liidetav 5? Võtmeks: definitsiooni järgi ...vastab absoluutne tähesuurus tähele, mis asub vaatlejast 10 pc kaugusel. Valgustatus teatavasti kahaneb pöördvõrdeliselt kauguse ruuduga.

[ Peatüki indeks | Õpiku tekst | Illustratsioonid | Viited | Kordamisküsimused ]

Õpiku tegijad / opik@obs.ee
© Tartu Tähetorni Astronoomiaring 1997-98

17. juuli 1998

 [Avatud Eesti Fond]

Selle õpiku valmimist on toetanud Avatud Eesti Fond.