5. osa: Universum

1. peatükk: Lõpmatus

Võtame viimast korda kokku teadmised "kogu maailmast". Kunagi oli see tükike põldu-metsa, taevakuppel koos päikese, kuu ja tähtedega selle kohal. Siis korrapärane kera, selle ümber taevased sfäärid Päikese, Kuu ja planeetide tarbeks, kinnistähtede kristallsfäär neid kõiki ümbritsemas. Seejärel kosmose ääretu tühjus, kus ümber Päikese-tähe tiirlevad Maa-sarnased planeedid, hirmkaugel üksteisest ning siiski nii lähedal, kui võrrelda teiste tähtedega. Tähtedega, mis samuti on kauged päikesed, ja mille ümber võivad samuti tiirelda omad planeedid. Ja nüüd lõpuks teadmine, et seegi uskumatult suur tähesüsteem, meie Galaktika, kus arvatakse olevat sada miljardit tähte, on vaid tolmukübe veelgi ääretumas ilmaruumis. Ruumis, kus kõikjal on samasugused galaktikad, ükskõik, mis suunas ja kui kaugele me ka ei vaataks.

Inimkond on seda laadi nähtuste iseloomustamiseks välja mõelnud sõna "lõpmatus". Kõigis keeltes -- ladina-inglise infinity, saksa Unendlichkeit -- on see termin kujundatud eituse baasil: "see, millel ei ole lõppu". Termin ise on puht-filosoofiline. Igapäeva-elus me seda ei vaja, kuna maailmas ei ole lõpmatuid asju. Välja arvatud Universum. Kuidas inimene mõistab lõpmatust? Ka seda on uuritud, ja sel on kindel vastus: inimene tajub lõpmatust ainult numbriliselt, mingi igapäevase lõpliku nähtuse lõputu kordumise kaudu. Lõpmata pikk aeg on see, kui igale päevale järgneb alati samasugune päev. Lõpmatu tee on see, kui igale läbikäidud kilomeetrile järgneb jälle samasugune kilomeeter. "Rumal lõpmatus", nagu seda mõnikord nimetatakse. Juba vana-aja filosoofid teadsid, kuidas sellist lõpmatust "ära narrida". Juhime teeraja otsad kokku, saame lõputa tee. Painutame tasandi kerapinnaks -- sfääriks ja saame lõpmatu pinna. Võib-olla õnnestub ka ruumi kuidagiviisi painutada, et sealgi kogu aeg ühes suunas liikudes samasse kohta tagasi jõuaks. Ainult aja otsi ei anna kokku painutada (ulmelugudes saadakse ka sellega hakkama). Eesti Õigekeel ütleb, et sellised süsteemid (ringrada, kerapind, kõverruum) on küll piiritud, aga mitte lõpmatud. Milline on õige lõpmatus, seda Õigekeel ei tea. 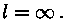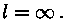Matemaatikud teavad: lõpmatu joon on see, mille pikkus on Lõpmatu pind see, kus pindala Lõpmatu ruum ... (mõelge ise välja!). Aga matemaatikud teavad ka seda, et lõpmata pikka joont annab mahutada lõpliku suurusega pinnale, lõpmatut pinda lõpliku suurusega ruumiossa jne. Kas saime targemaks?

Joonis 1. Toomas Vint. Lõpetamata maastik. Näide "rumalast lõpmatusest". Joonis 2. Lõputa tee -- Pirita ringrada. Joonis 3. Lõputa pind -- Möbiuse leht.

[ Peatüki indeks | Õpiku tekst | Illustratsioonid | Viited | Kordamisküsimused ]

• Eelmine peatükk: Galaktikate ruumjaotus
• Järgmine peatükk: Kosmoloogiline printsiip
• Sisukord

Õpiku tegijad / opik@obs.ee © Tartu Tähetorni Astronoomiaring 1997-99 12. märts 1999

Selle õpiku valmimist on toetanud Avatud Eesti Fond.